Distribución de probabilidad continua uniforme

La distribución uniforme es aquella que puede tomar cualquier valor dentro de un intervalo, todos ellos con la misma probabilidad.

Es una distribución continua porque puede tomar cualquier valor y no únicamente un número determinado (como ocurre en las distribuciones discretas).

La distribución Uniforme es el modelo continuo más simple. Corresponde al caso de una variable aleatoria que sólo puede tomar valores comprendidos entre dos extremos a y b, de manera que todos los intervalos de una misma longitud (dentro de (a, b)) tienen la misma probabilidad. También puede expresarse como el modelo probabilístico correspondiente a tomar un número al azar dentro de un intervalo (a, b).

En teoría de probabilidad y estadística, la distribución uniforme continua es una familia de distribuciones de probabilidad para variables aleatorias continuas, tales que para cada miembro de la familia, todos los intervalos de igual longitud en la distribución en su rango son igualmente probables. El dominio está definido por dos parámetros, a y b, que son sus valores mínimo y máximo. La distribución es a menudo escrita en forma abreviada como U(a,b).

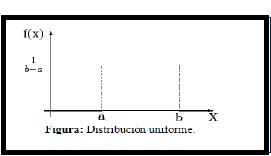
En resumen:

• Es la más simple de todas las distribuciones continuas de probabilidad.
• Se caracteriza por una función de densidad que es “plana”, y por ello la probabilidad es uniforme en un intervalo cerrado.
• La función de densidad de la variable aleatoria uniforme continua X en el intervalo [A,B] es:

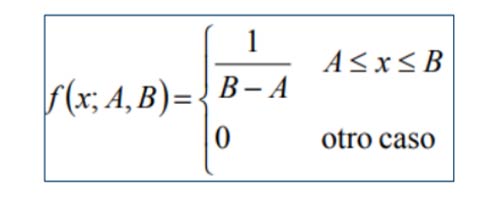
• La media y la varianza de la distribución uniforme continua ʄ (x;A,B) son:

• La distribución uniforme a menudo se llama distribución rectangular.
• Es sencillo calcular las probabilidades para la distribución uniforme debido a la naturaleza simple de la función de densidad.
• Sin embargo, la aplicación de esta distribución se basa en la suposición de que la probabilidad de caer en un intervalo de longitud fija dentro de [A,B] es constan

Propiedades

Media

Medida de tendencia central:

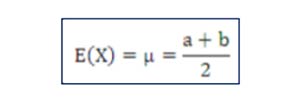
Varianza

Medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media. O en pocas palabras, la media de los residuos al cuadrado.

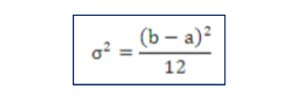
Desviación Estándar

Medida de dispersión para variables de razón (variables cuantitativas o cantidades racionales) y de intervalo. Se define como la raíz cuadrada de la varianza de la variable.

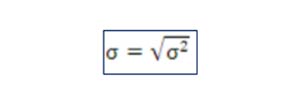
Si quieres conocer otros artículos parecidos a Distribución de probabilidad continua uniforme puedes visitar la categoría .