4 Reglas algebraicas básicas

Las 4 reglas algebraicas básicas son operaciones fundamentales utilizadas en álgebra para combinar, simplificar y manipular términos. Estas reglas incluyen la suma (+), resta (-), multiplicación (×) y división (÷). La suma combina términos, la resta los sustrae, la multiplicación los multiplica y la división los divide. Estas reglas son clave para simplificar expresiones algebraicas y resolver ecuaciones en álgebra.

Reglas algebraicas básicas para cualquier tipo de operación

Se considerar a estas reglas como las más usadas para la resolución de operaciones matemáticas con expresiones algebraicas.

Regla de los signos

• Suma de números con signos iguales: se suman los valores absolutos y se conserva el signo común.
• Suma de números con signos opuestos: se resta el valor absoluto más pequeño del más grande y se conserva el signo del número con mayor valor absoluto.
• Resta: se puede convertir en una suma cambiando el signo del número que se está restando.
• Multiplicación y división: la multiplicación o división de números con signos iguales da como resultado un número positivo, mientras que la multiplicación o división de números con signos opuestos da como resultado un número negativo.

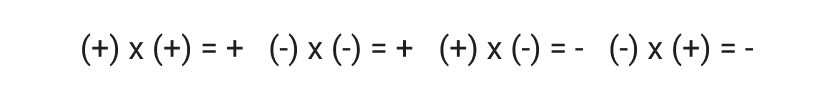
La regla de la potencia

Cuando se trabaja con potencias, se aplican las siguientes reglas:

• Potencia de un número: Al elevar un número a una potencia, se realiza la multiplicación del número por sí mismo tantas veces como indique el exponente. Por ejemplo, a^n implica multiplicar a por sí mismo n veces.
• Producto de potencias con la misma base: Al multiplicar potencias que tienen la misma base, se suman los exponentes. Por ejemplo, a^n × a^m es igual a a^(n+m).
• Cociente de potencias con la misma base: Al dividir potencias que tienen la misma base, se restan los exponentes. Por ejemplo, a^n ÷ a^m es igual a a^(n-m).
• Potencia de una potencia: Al elevar una potencia a otra potencia, se multiplican los exponentes. Por ejemplo, (a^n)^m equivale a a^(n×m).

La regla de coeficientes

La regla de coeficientes es una regla en álgebra que se aplica al multiplicar o dividir términos que tienen coeficientes numéricos. En resumen:

• Producto de coeficientes: Al multiplicar términos que tienen coeficientes numéricos, se multiplican los coeficientes entre sí. Por ejemplo, 2x * 3y = 6xy.
• División de coeficientes: Al dividir términos que tienen coeficientes numéricos, se divide el coeficiente del numerador entre el coeficiente del denominador. Por ejemplo, (4xy) / (2x) = 2y.

La regla de coeficientes permite simplificar y realizar operaciones con términos que tienen coeficientes numéricos, facilitando el cálculo algebraico.

La regla de Ruffini

La regla de Ruffini, también conocida como el método de división sintética, es un procedimiento utilizado para dividir un polinomio por un binomio de la forma (x - a). En resumen:

1. Se escribe el polinomio en forma descendente de exponentes y se identifican los coeficientes de cada término.
2. Se coloca el valor "a" en el divisor (x - a) y se realiza la división sintética.
3. Se continúa dividiendo hasta obtener el cociente y el resto, que representan la expresión simplificada del polinomio original.

La regla de Ruffini es una herramienta útil para simplificar y dividir polinomios, permitiendo encontrar soluciones y factores de manera eficiente.

Si quieres conocer otros artículos parecidos a 4 Reglas algebraicas básicas puedes visitar la categoría .