Matemáticas Financieras: Anualidades

Se llama serie uniforme o anualidad a un conjunto de pagos iguales y periódicos Aquí el término de pagos hace referencia tanto a ingresos como egresos De la misma manera, el término anualidad se utiliza para indicar que los pagos son periódicos y no necesariamente cada año Los períodos pueden ser el día, la semana, la quincena, etc.

Tipos de Anualidades

• Vencidas
• Anticipadas
• Diferidas
• Perpetuas

Anualidades Vencidas

Se llama anualidad vencida a aquella en donde el pago se hace al final del período de pago.

Ejemplo de Anualidades vencidas

El salario mensual de un empleado, las cuotas mensuales iguales y vencidas en la adquisición de un vehículo o de electrodoméstico por el sistema de financiación, etc.

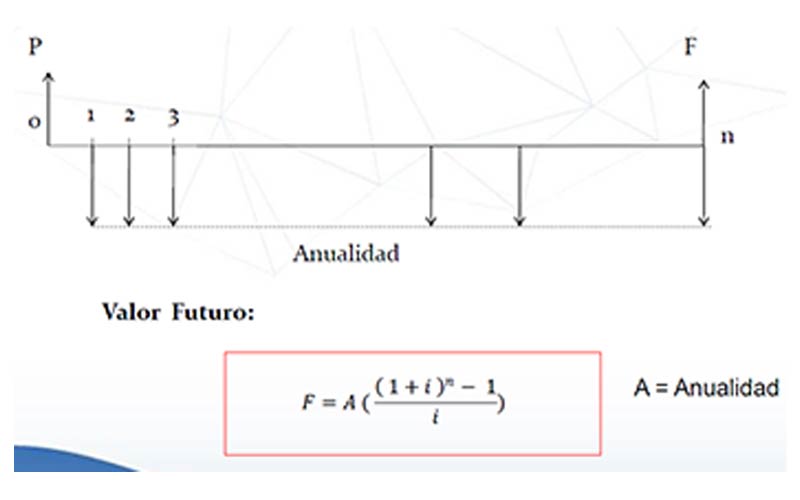
Ejemplo 1:

Durante un año y medio se hacen depósitos por mes vencidos de $12.000 cada uno en una institución de ahorro que paga un interés de 3% mensual. Calcule la suma total acumulada en las cuenta de ahorro al final de este período.

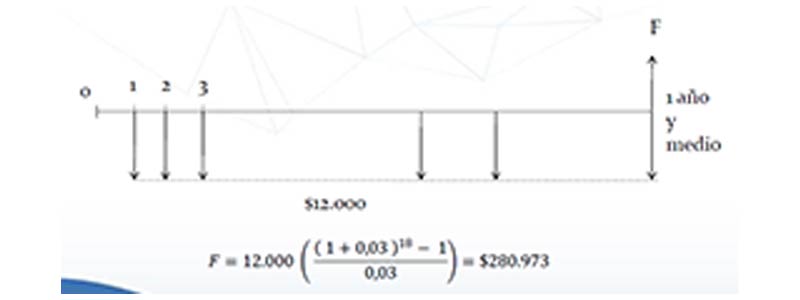
Ejemplo 2

El curso de administración de empresa decide depositar en una cuenta de ahorro durante 16 meses por un valor equivalente a 45 250 cada fin de mes para realizar una despedida a los alumnos egresados Si la entidad financiera paga por los depósitos 12 de interés efectivo trimestral.

Cuanto dinero se reúne al final del período

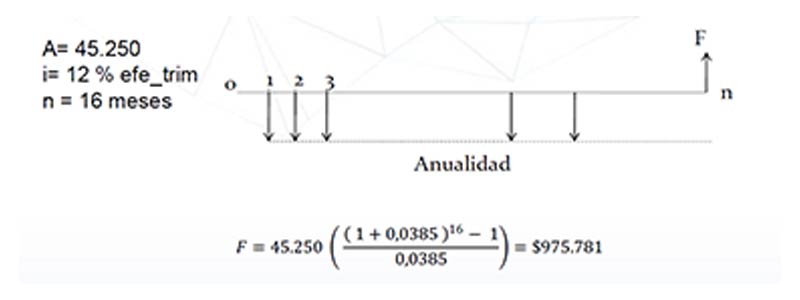
Anualidades anticipadas

En los negocios, es frecuente que los pagos periódicos se efectúen al comienzo de cada período Anualidad Anticipada tal es el caso de la renta de terrenos, edificios oficinas y cuyo alquiler se paga al principio de cada período Otros ejemplos son seguros de bienes en general, seguros de vida, etc

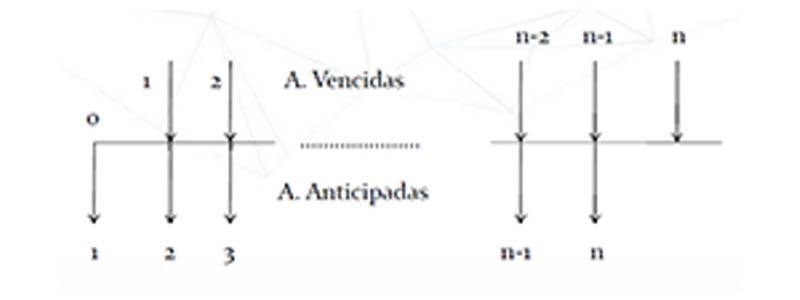
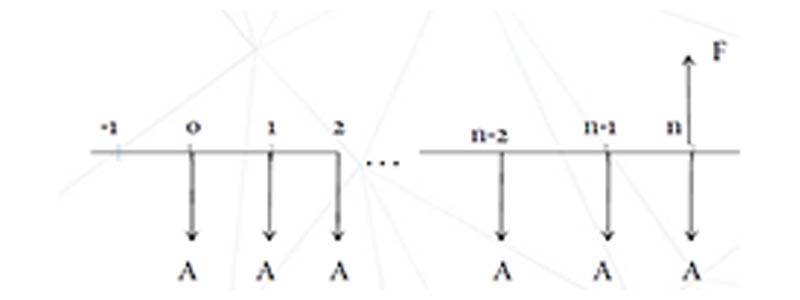
Observe que al agregar un último pago A se obtiene el valor futuro de una anualidad vencida A, por período, pagadera durante n+1 períodos. Restando el último pago A, el cual se había agregado, se obtiene el valor futuro de una anualidad anticipada A, pagadero durante n período; ( (F/A, i%, n + 1) – 1 ).

Valor Futuro de una Anualidad Anticipada

Valor Presente de una Anualidad Anticipada

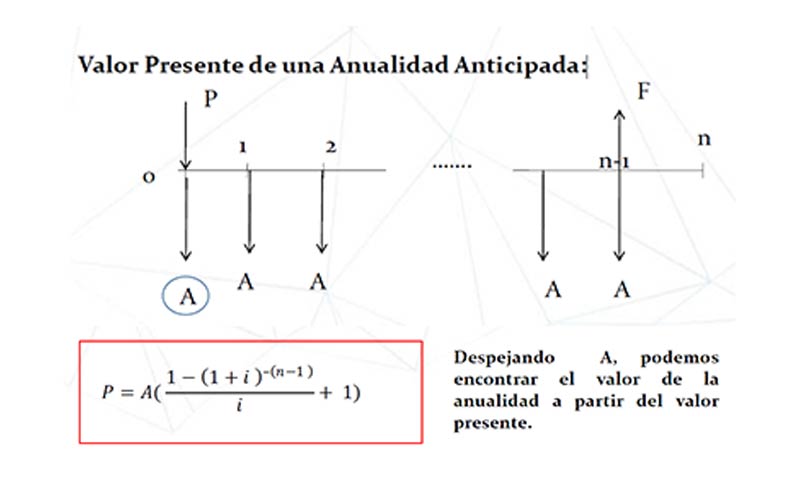
Anualidades Diferidas

En los negocios, es frecuente que algunas circunstancias obliguen a que los primeros períodos de pago comience en una fecha futura, hasta después de transcurrido cierto tiempo desde el momento inicial o de convenio Es decir, la fecha inicial de la anualidad no coincide con la fecha del primer pago En estos casos, se dice que la anualidad es diferida

Para el cálculo de los valores de las anualidades diferidas no se requieren nuevas fórmulas Para desarrollar este tipo de problemas es necesario analizar los problemas utilizando diagramas que le permita determinar, cuidadosamente, el tiempo diferido y el tiempo de pago, para luego plantear las ecuaciones de equivalencia que conducen a la correcta solución

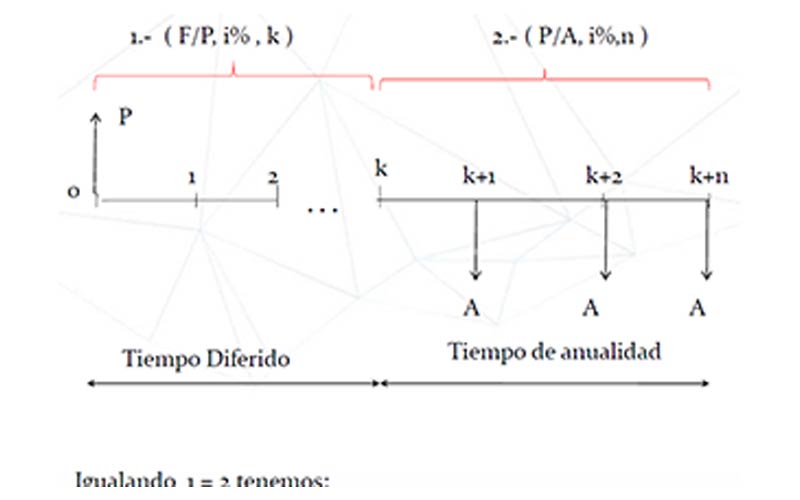
Anualidades Perpetuas

En los negocios, es frecuente que ciertas rentas, salvo sucesos imprevistos, se paguen indefinidamente Entre muchas otras, las rentas que se pagan a perpetuidad son renta de un terreno, los legados por instituciones de beneficencias, los dividendos sobre acciones preferentes, las sumas que es necesario reservar cada año para proveer la reposición de un puente, etc

Definición: Una renta perpetua es una anualidad cuyo plazo no tiene fin.

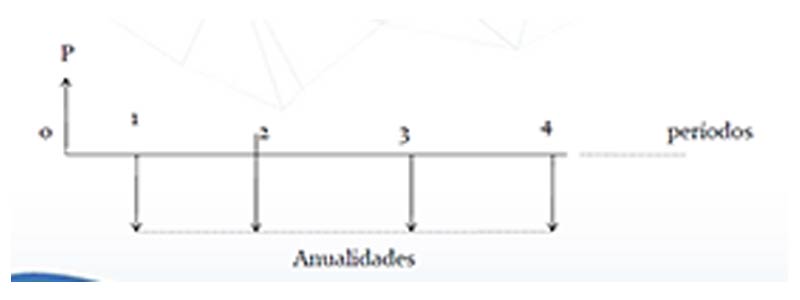
Se deduce que el valor presente de la renta perpetua es aquella cantidad p que, en un período, produce como intereses la suma A, o sea:

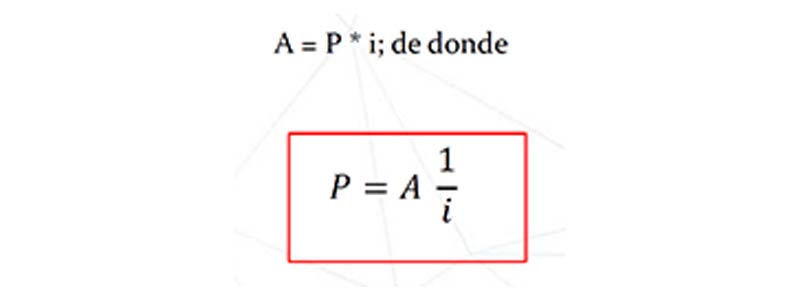
El factor 1/i = (P/A, i%, ∞ ), es el valor presente de una renta perpetua vencida de una unidad monetaria por período, a la tasa i por período.

Valor presente de las rentas perpetuas simple anticipada

Cuando el pago de la renta es inmediato, al trazar el diagrama se observa que el valor actual es equivalente al de una renta perpetua vencida, aumentada en el primer pago que debe efectuarse de inmediato.

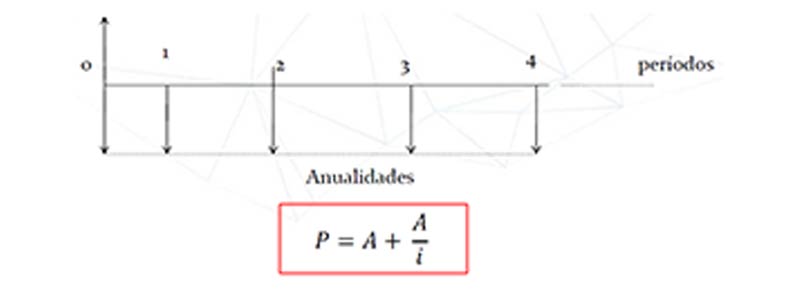
Si el pago que debe efectuarse de inmediato es W distinto de A, se tiene, para el valor actual:

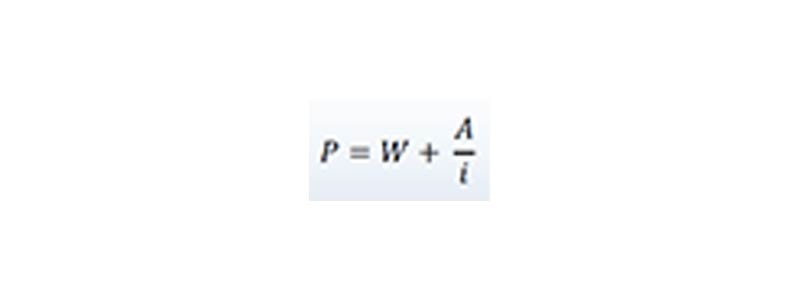
Si quieres conocer otros artículos parecidos a Matemáticas Financieras: Anualidades puedes visitar la categoría .