Unión e intersección de conjuntos
La unión e intersección de conjuntos son uno de los cálculos más utilizados para ver el comportamiento de diversos conjuntos
¿Qué es unión de conjuntos?
La unión de conjuntos es una operación que combina todos los elementos únicos de dos o más conjuntos en un nuevo conjunto.
![\[ \ A\cup B=\left\{x|x\ \in A\ \vee x\in B\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-5c68f106212f4d4aaa3ba78a105b2d08_l3.png "Rendered by QuickLaTeX.com")
En este caso podemos ver que la unión de dos conjuntos A y B forman un conjunto compuesto por los elementos que pertenecen a A y los elementos que pertenecen a B.
Lo anterior se lee de la siguiente manera: A unido a B, está formado por todos los elementos x, tal que x pertenece a A o x pertenece a B.
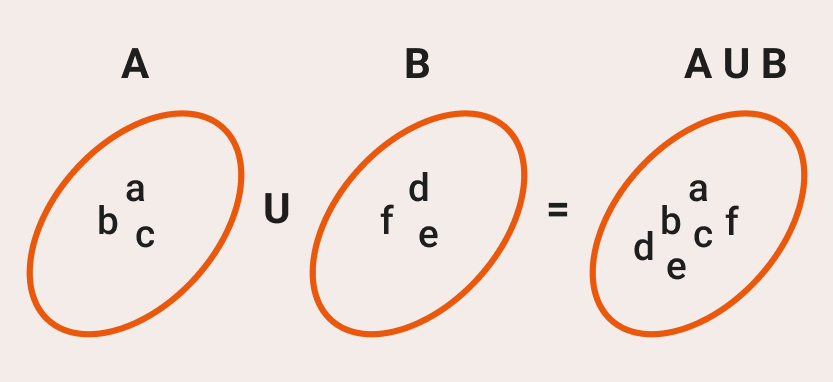
Esta es su representación gráfica.
![\[ \ A=\left\{a,\ b,\ c\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-704f2f54d0dd5d6cdc5a8d02fc36fbf9_l3.png "Rendered by QuickLaTeX.com")
![\[ \ B=\left\{d,\ e,\ f\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-b4f242d247f5758eb5f6ec86bda40e86_l3.png "Rendered by QuickLaTeX.com")
![\[ \ A\cup B=\left\{a,\ b,c,d,e,f\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-5faf97bac56706bba373d5cccfa0d3b5_l3.png "Rendered by QuickLaTeX.com")
Propiedades de la unión de conjuntos:
- Conmutativa: El orden de la unión no importa. A ∪ B = B ∪ A.
- Asociativa: La forma en que se agrupan los conjuntos no afecta el resultado. (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Identidad: La unión de un conjunto con el conjunto vacío no cambia el conjunto original. A ∪ ∅ = A.
- Absorción: Unir un conjunto con su subconjunto no altera el conjunto original. A ∪ (A ∩ B) = A.
- Ley de De Morgan: La unión de los complementos de conjuntos es igual al complemento de la intersección de los conjuntos. (A ∩ B)' = A' ∪ B'.
¿Qué es intersección de conjuntos?
La intersección de conjuntos es una operación que devuelve un nuevo conjunto que contiene únicamente los elementos comunes a dos o más conjuntos. Es decir, se seleccionan aquellos elementos que están presentes en todos los conjuntos involucrados en la operación de intersección.
![\[ \ R\cap\ S=\left\{x|x\in R\land x\in S\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-33af1381de8a5173c9d8b4c5473a919e_l3.png "Rendered by QuickLaTeX.com")
Por ejemplo: dados los conjuntos R = {1,2,3,4} y el conjunto S = {3,4,5,6}, podríamos decir que la intersección seria:
![\[ \ R\cap\ S=\left\{3,4\right\} \]](https://www.matemente.com/wp-content/ql-cache/quicklatex.com-021799ac1f6963eb7b90a54ca786c7fd_l3.png "Rendered by QuickLaTeX.com")
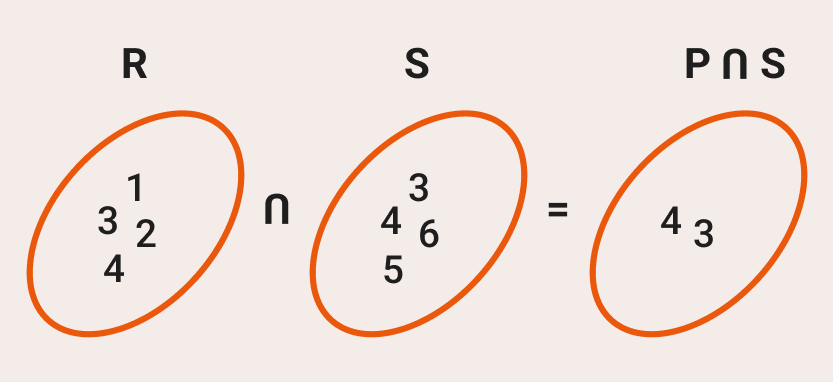
Propiedades de la intersección de conjuntos
La propiedad de idempotencia establece que la intersección de un conjunto con sí mismo es igual al conjunto original. En otras palabras, al intersectar un conjunto consigo mismo, el resultado sigue siendo ese mismo conjunto.
Además, si realizamos la intersección entre el conjunto universal "U" y uno de sus subconjuntos "P", el resultado será simplemente el subconjunto "P".
Si quieres conocer otros artículos parecidos a Unión e intersección de conjuntos puedes visitar la categoría .
Deja una respuesta
También Puedes Leer